Inverse design via machine learning

Recenty there are many ongoing work on applying machine learning (ML) to mechanics, which primarily focus on predicting mechanial properties and stress-strain relationship. Here, we take ML furhter by applying it to design soft membranes. One direct application of our machine learning design approach is for designing inflated membranes with specified contacts (i.e., 3D target shape) which is important for developing mechanotherapy devices.

Thermalized Euler Buckling

Recently there has been great interests in utilizing thin elastic sheets for engineered materials. Foppl van Karman number vK=$YL^2/\kappa$, ratio between Young’s modulus $Y$ multiply by system’s dimensions $L^2$ and bending rigidity $\kappa$, is often used to characterized “thinness” or how easy the materials are to bend relative to stretching. Many studies have shown that introducing altrenating cuts, known as “kirigami cuts”, can prevent failure as the sheet can buckle out of the plane and its joint components can bend in-plane like hinges. Under stretching thin elastic sheets will experience compression in the direction perpendicular to the loading and we can think this as a 1D Euler buckling problem. In our previous work (see my other post or my paper [2]), we indeed find a universality relationship between buckling and stretching (compression perpendicular to loading) of thin elastic sheets with a single slit from the macro (cm size) to nano scale. I want to note in that work [2] the nano sheets (graphene and MoS2) are stretched at a very low temperature 4.2 K. Most of mechanical devices (actuators) are working preferably at room temperature 300 K. It was found that the bending rigidity (at long wave length) of graphene increases by more than 1000 at room temperature relative to its zero temperature value due to thermal fluctuations. This bending stiffening is similar to how a perfectly smooth A4 paper sheet can easily bent (cannot hold its own weight), whereas a flattened crumpled A4 paper with random corrugations can hold a pen! In this work I will address how temperature affects Euler buckling using mean field theory and tested on molecular dynamics similations.

Forward and inverse design for structural design via supervised autoencoder

Recently, there has been great interests in applying mechanine learning to design composite materials. Early studies in optimizing materials properties usually use a supervised machine learning (ML) model as a forward solver. Typically, a supervised ML model is trained with a very large datasets and then the supervised model is used to predict materials outside the traning sets. Another approach is to train a supervised model iteratively with small datasets, similar to optimization tool such as genetic algorithm or greedy algorithm, and ask the model to generate superior designs. More details can be found in my paper[1] or my other post on using CNN to search optimal kirigami design.

Machine learning for designing stretchable graphene kirigami

Visualization of graphene membrane.

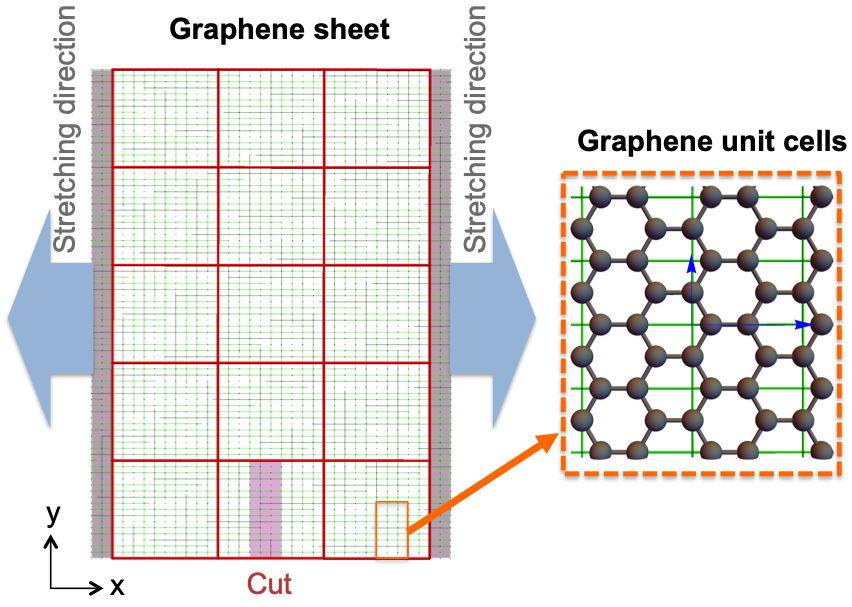Recently, there has been great interests in using patterned cuts, often called kirigami cuts, to design stretchable materials. Introducing cuts allow thin materials (membranes) to extend reaching a fracture strain beyond its pristine value. This topology optimization problem is highly complex and an analytical approach is only available for simple cases (e.g few cuts). Using standard computational approaches (e.g. molecular dynamics) to simulate all candidate designs is not practical, as the number of possible ways to pattern the 2D materials grows exponentially with system size. To solve this problem, I use a machine learning (ML) approach, where data are used to provide physical insights and an effective model to describe a physical system.

2D Ferroelectric Rashba Lead Chalcogenides

Monolayers and heterostructures of 2D electronic materials with spin-orbit effects offer promise for observing many novel physical effects. For instance, topological insulators or Rashba semiconductors coupled with a superconductor may host Majorana fermions, which are the building blocks for quantum computers. In this research, we found ferroelectric Rashba buckled lead chalcogenides monolayers. Because of the inversion symmetry breaking (out-of-plane buckling) and the heavy lead element with strong spin-obit interaction, this class of materials is ferroelectric and possesses giant Rashba splitting and belongs to a new class of matters, the ferroelectric Rashba semiconductors (FERSC). FERSC is particularly attractive for spintronic applications as the Rashba spin-texture can be switched in a non-volatile way by external electric fields or mechanical strains.

Valley and ferroelectric switching in MX monochalcogenide monolayers (M=Sn, Ge; X=S, Ge)

Transition metal dichalcogenides (TMDCs) have been studied extensively and have shown potential for many technological applications ranging from photovoltaics to valleytronic devices. Despite of the fast growth of generated data, currently at ~2.5 quintillion bytes of data per day, there have been only few developments on applications of 2D materials for memory devices.

Kirigami actuators

Cooperative Dynamics and Interfacial Scales in Glass Forming Liquids

Ultra-thin polymer films and polymer nanocomposites have ubiquitous technological applications, ranging from electronic devices to artificial tissues. These nanoconfined polymer materials, typically with thickness less than 100 nm, exhibit properties that are different from their bulk counterparts. To engineer the dynamics, e.g. glass transition temperature $T_g$, remains a technological challange because lack of fundamental understanding of glass formations in polymer melts under naoconfinements.