Machine learning for designing stretchable graphene kirigami
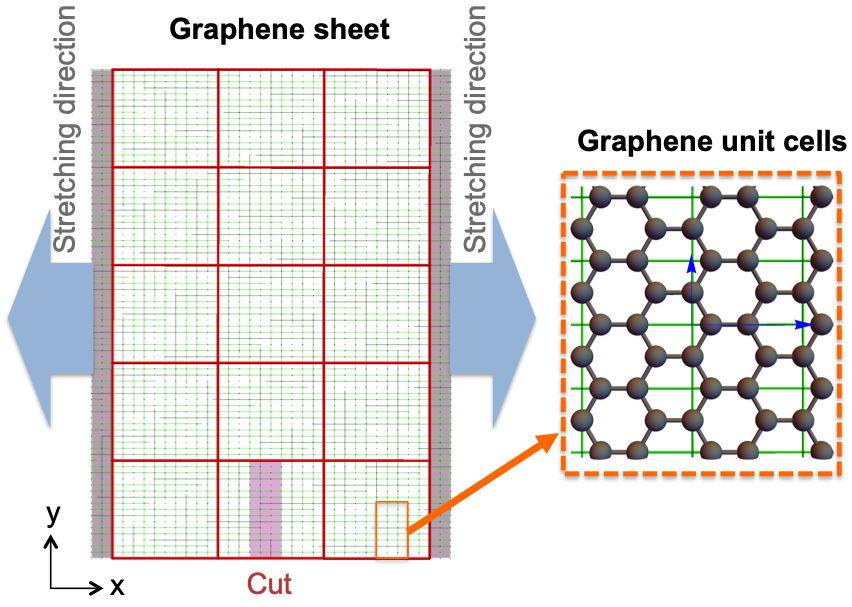 |
Recently, there has been great interests in using patterned cuts, often called kirigami cuts, to design stretchable materials. Introducing cuts allow thin materials (membranes) to extend reaching a fracture strain beyond its pristine value. This topology optimization problem is highly complex and an analytical approach is only available for simple cases (e.g few cuts). Using standard computational approaches (e.g. molecular dynamics) to simulate all candidate designs is not practical, as the number of possible ways to pattern the 2D materials grows exponentially with system size. To solve this problem, I use a machine learning (ML) approach, where data are used to provide physical insights and an effective model to describe a physical system.
Before going to deep learning, we may consider the simplest approach which is linear model: \(f(\pmb{x})=\beta_0+\sum_i\beta_ix_i+\sum_{i\leq j}\beta_{ij}x_ix_j+\sum_{i\leq j\leq k}\beta_{ijk}x_ix_jx_k+\dots\,.\)
Linear model (with feature transformation) works reasonably efficient for small system; however, for finer grids (or larger systems), the number of parameters will increase significantly as there will be $(n+d)!/(n!d!)\sim n^d/d$ of $\beta$ terms, where $d$ is the polynomial degree, $n$ is number of grids (features). Let us suppose we use one rectangular graphene unit cell as the size of one grid. For a system size $\sim100\times200$ Angstrom, the input size is $30\times80=2400$ ($10\times16$ rectangular graphene cells in each coarse grid), at a polynomial degree of 3, we will need $\sim10^9$ parameters to fit.
Locality and Convolutional Neural Networks
In the series expansion approach, the 2D cut patterns are flattened into a 1D-array and thus some of the local spatial information are lost. Series expansion can be used to “recover” the information of interactions between neighbors, but this approach becomes inefficient when the number of cells becomes large. This series expansion approach is computationally inefficient as we expect the interactions should be local. In principle, one could do series expansions to the nearest neighbors only; however, details of the potentials are not always known. For these reasons, the convolutional neural networks (CNN) is a more appropriate and scalable model as this deep learning is superior in recognizing edges in 2D motifs as well as performing down-sampling, which is very suitable for our problem. In the CNN, the 2D image (input) is convolved by a set of learnable filters and this allows the model to learn 2D motifs. An image passing through these filters then activates neurons which then classify (or rank) the cutting patterns to good or bad designs. This approach is more efficient than the series expansion approach as the CNN model is built based on learned 2D local motifs.
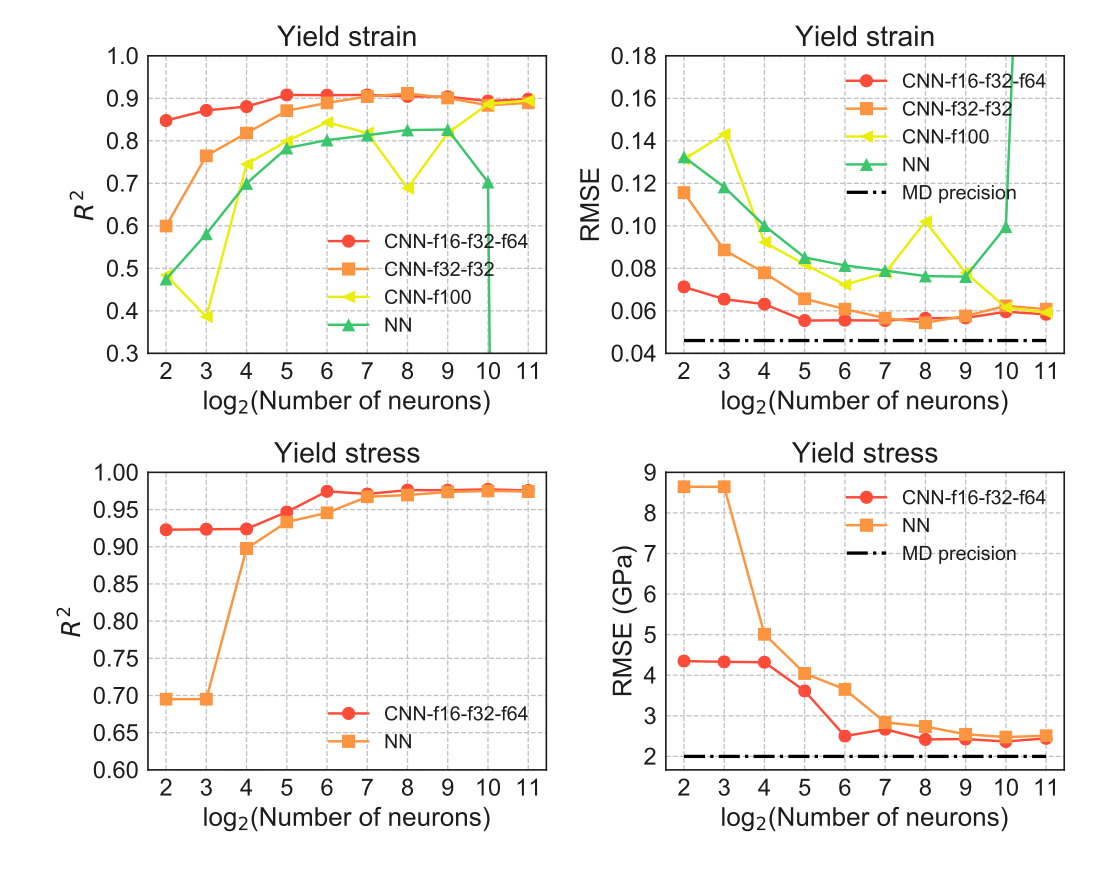 |
We benchmark accuracy score of linear model, neural networks (NN) and convolutional neural netwroks (CNN). We found that the CNN with deep architecture performs the best.
CNN for search algorithm
Next we developed a simple CNN search algorithm. Search algorithm:
- Start with a random population
- Evaluate targert properties with MD
- Train CNN
- Use CNN to predict the unexplored configurations
- Sort and take the top 100 candidates for the next generation
- Back to 2
The CNN search algorithm is able to search for the optimal solutions with only 1000 training data in a large design space of approximately 4,000,000. The superior designs for each generation are shown bellow.
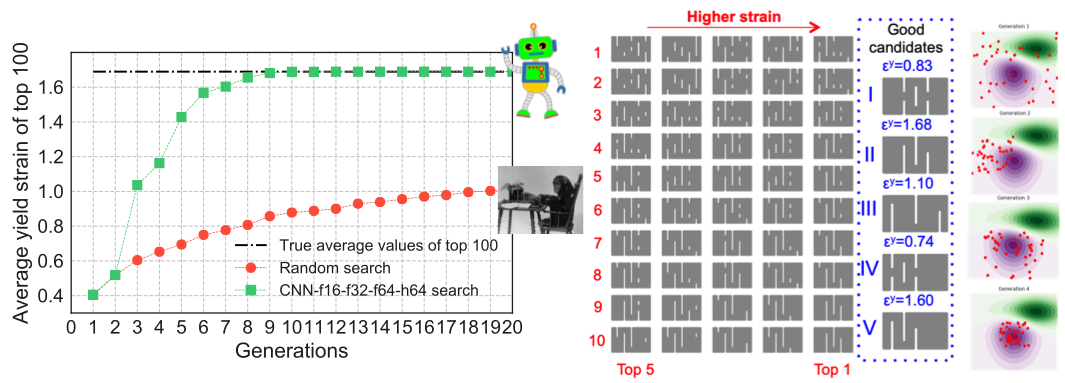 |
To be continued ..
References: [1] P. Z. Hanakata, Ekin D. Cubuk, David K. Campbell, and Harold S. Park, Phys. Rev. Letter, 121, 255304 (2018). [2] Paul Z. Hanakata, Ekin D. Cubuk, David K. Campbell, and Harold S. Park, arxiv.org/abs/1808.06111.
Some of the analysis and TensorFlow codes are avalaible in my GitHub page: https://github.com/phanakata/ML_for_kirigami_design