Thermalized Euler Buckling
Recently there has been great interests in utilizing thin elastic sheets for engineered materials. Foppl van Karman number vK=$YL^2/\kappa$, ratio between Young’s modulus $Y$ multiply by system’s dimensions $L^2$ and bending rigidity $\kappa$, is often used to characterized “thinness” or how easy the materials are to bend relative to stretching. Many studies have shown that introducing altrenating cuts, known as “kirigami cuts”, can prevent failure as the sheet can buckle out of the plane and its joint components can bend in-plane like hinges. Under stretching thin elastic sheets will experience compression in the direction perpendicular to the loading and we can think this as a 1D Euler buckling problem. In our previous work (see my other post or my paper [2]), we indeed find a universality relationship between buckling and stretching (compression perpendicular to loading) of thin elastic sheets with a single slit from the macro (cm size) to nano scale. I want to note in that work [2] the nano sheets (graphene and MoS2) are stretched at a very low temperature 4.2 K. Most of mechanical devices (actuators) are working preferably at room temperature 300 K. It was found that the bending rigidity (at long wave length) of graphene increases by more than 1000 at room temperature relative to its zero temperature value due to thermal fluctuations. This bending stiffening is similar to how a perfectly smooth A4 paper sheet can easily bent (cannot hold its own weight), whereas a flattened crumpled A4 paper with random corrugations can hold a pen! In this work I will address how temperature affects Euler buckling using mean field theory and tested on molecular dynamics similations.
Here are the main takeaways of our findings:
- Buckling at finite temperature is not stationary and we thus need statistical mechanics
- We use a mean field theory approach to describe buckling and find similar Euler critical buckling expression but with renormalized elastic constants
- Similar to critical phenomena in magnetic systems, we also find that the height center of mass can be used as an oorder parameter
- We indeed find magnetic-like transitions with \(\beta=1/2\) and we also find that the susceptibility height center of mass shows a diverging trend (similar to magnetic susceptibiliy) near the buckling transition
- We also use pertubing field to detect buckling
- We find that elastic constants (Young’s modulus, bending rigidty, critical buckling strain) become temperature dependent once the system becomes comparable to thermal length. All details can be found in our paper [1]!
Buckling at finite temperature
Mean field theory
Universality in thermalized buckling transition
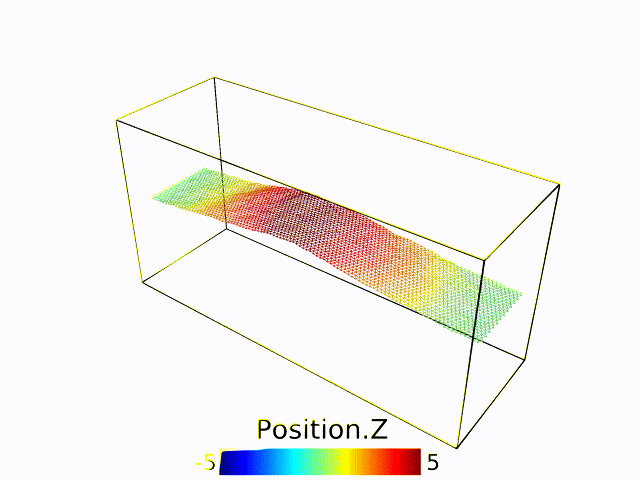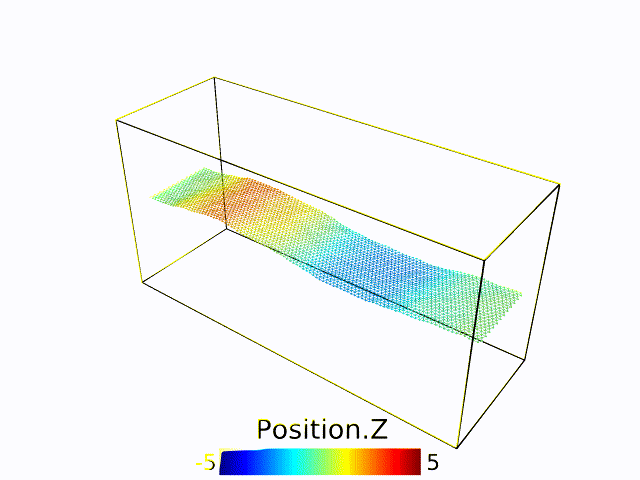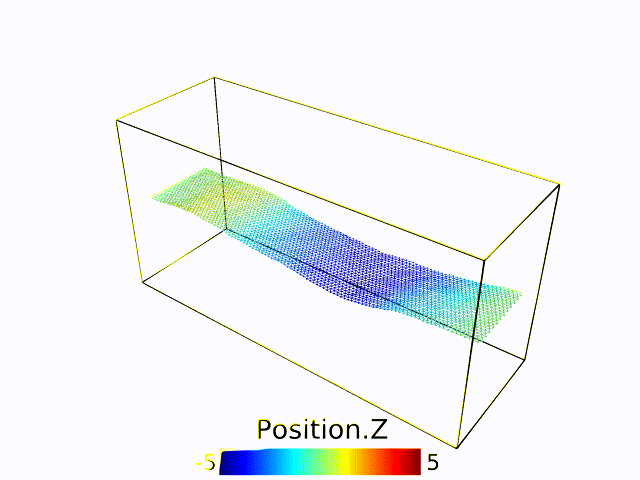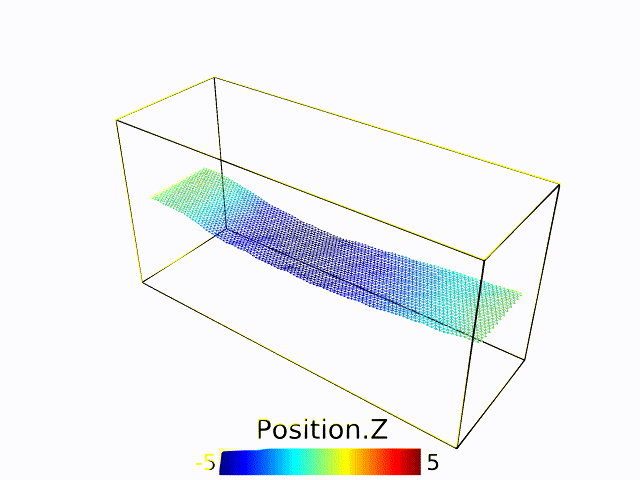
To be continued
Final notes
This work was in collaboration with Mark Bowick’s group at UCSB. If you want to use our pictures or animations for your research please send me an email and I am more than happy to provide the files and also cite our paper [2].
References: